Computing Bond Yield with Newton’s Method

On August 31, 2015August 3, 2016 By ElenaIn Numerical Analysis

In fixed income analysis it is often required to calculate the yield of some coupon paying instrument, for example a bond. Very simply, an yield of a bond is defined as a single rate of return. Under continuous compounding, given a set of interest rates $\{r_{T_1}, r_{T_2}, ..., r_{T_n}\}$ , the yield $y$ equates the present value of the bond computed under a given set of rates. In other words:

$\sum_{i=1}^{n}exp(-r_{T_i}T_i) C_{T_i}=\sum_{i=1}^{n}exp(-yT_i) C_{T_i}$

where $C_{T_i}$ is a coupon paid out at time $T_i$ . Usually, one solves for $y$ using some iterative guess-work, e.g. goal seek. In this post I will show you a well-know Newton’s recursive method that can be used to base such goal seek on.

The Newton’s Method

The Newton’s method is based on a recursive approximation formula:

$x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}$

Let $B=\sum_{i=1}^{n}exp(-yT_i) C_{T_i}$ be the price(or present value) of the bond expressed via its yield. Then, taking $x$ to represent interest rate, we have:
$f(x) = \sum_{i=1}^{n}exp(-x_{T_i}T_i) C_{T_i} - B = 0$ and $f'(x)=-\sum_{i=1}^{n}T_i C_{T_i} exp (-x_{T_i}T_i)$

The recursive formula to solve for yield becomes:

$x_{i+1}=x_i+\frac{\sum_{i=1}^{n}exp(-x_{T_i}T_i) C_{T_i} - B}{\sum_{i=1}^{n}T_i C_{T_i} exp (-x_{T_i}T_i)}$

Goal Seek in C#

Now let’s take a look at an example implementation. The while loop in CalculateYield method implements the goal seek. This is a very simple example, and we pretend to have the bond price.

using System;
using System.Collections.Generic;
using System.Linq;

namespace YieldCalculator
{
    class EntryPoint
    {
        static void Main(string[] args)
        {
            // use some numbers to illustrate the point
            // maturities in months
            int[] maturities = { 6, 12, 18, 24, 30, 36 };
            double[] yearFrac = maturities.Select(i => i / 12.0).ToArray();
            // bond principle
            double P = 100;
            // bond price
            double B = 108;
            double couponRate = 0.1;
            // calculate future cashflows
            double[] cashflows = maturities.Select(i => (P * couponRate) / 2.0).ToArray();
            // add principle repayment
            cashflows[cashflows.Count() - 1] = P + cashflows[cashflows.Count() - 1];

            double initialGuess = 0.1;
            Console.WriteLine(CalculateYield(initialGuess, cashflows, yearFrac, B));
        }

        static double CalculateYield(double initialGuess, double[] cashflows, double[] yearFrac, double B)
        {
            double error = 0.000000001;
            double x_i = initialGuess-1.0;
            double x_i_next = initialGuess;

            double numerator;
            double denominator;
 
            while (Math.Abs(x_i_next - x_i) > error)
            {
                x_i = x_i_next;
                // linq's Zip is handy to perform a sum over expressions involving several arrays
                numerator = cashflows.Zip(yearFrac, (x,y) => (x * Math.Exp(y *-1*x_i))).Sum();
                denominator = yearFrac.Zip(cashflows, (x,y) => (x*y*Math.Exp(x*-1*x_i))).Sum();
                x_i_next = x_i + (numerator - B) / denominator;
            }
            return x_i_next;
        }
    }
}

Note how handy is LINQ’s Zip function to calculate a sum over an expression involving two arrays.

And now to the burning question – why the picture of a cat? The answer is even simpler than this post: It is a cute cat, so, why not?

Linear and Cubic Spline Interpolation

On June 7, 2015June 13, 2015 By ElenaIn Numerical Analysis1 Comment

In this post on numerical methods I will share with you the theoretical background and the implementation of the two types of interpolations: linear and natural cubic spline. These interpolations are often used within the financial industry. For example, discount rates for some maturity for which there is no point on an yield curve is often interpolated using cubic spline interpolation. Another example can be in risk management, like a position’s Value-at-Risk calculation obtained from a partial or a 2-dimensional revaluation grid.

Linear Interpolation

Let’s begin with the simplest method – linear interpolation. The idea is that we are given a set of numerical points and function values at these points. The task is to use the given set and approximate the function’s value at some different points. That is, given $x_i$ where $i=0,...,n-1$ our task is to estimate $f(x)$ for $x_0 \geq x\leq x_n$ . Of course we may require to go outside of the range of our set of points, which would require extrapolation (or projection outside the known function values).

Almost all interpolation techniques are based around the concept of function approximation. Mathematically, the backbone is simple:

$f(x)=y_{i}+\frac{y_{i+1}-y_i}{x_{i+1}-x_i} (x-x_i)$

The above expression tells us that the value of the function we are approximating at point x will be around $y_i$ and that $x_{i} \geq x\leq x_{i+1}$ . We can re-write this expression as follows:

$s_{k}(x)=a_{k}+b_{k}(x-x_{k})$

where we have substituted $y_{i}$ for $a_{k}$ and $\frac{y_{i+1}-y_i}{x_{i+1}-x_i}$ for $b_{k}$ . Our linear interpolation is now taking a form of linear regression around $a_{k}$ .

Linear interpolation is the most basic type of interpolations. It works remarkably well for smooth functions with sufficient number of points. However, because it is such a basic method, interpolating more complex functions requires a little bit more work.

Cubic Spline Interpolation

In what follows I am going to borrow a few formulations from a very good book: Guide to Scientific Computing by P.R.Turner. The idea of a spline interpolation is to extend the single polynomial of linear interpolation to higher degrees. But unlike with piece-wise polynomials, the higher degree polynomials constructed by the cubic spline are different in each interval $[x_i, x_{i+1}]$ . The cubic spline can be defined as:

$s_{k}(x)=a_{k}+b_{k}(x-x_{k})+c_{k}(x-x_{k})^{2}+d_{k}(x-x_{k})^{3}$

If you compare the above expression with the linear interpolation, you will see that we have added two terms to the rhs. It is these extra terms that should allow us achieve greater precision. There are certain requirements placed on s. These are: it must be continuous, and its first and second derivatives must exist. We only need to determine $b_{k}, c_{k}$ and $d_{k}$ coefficients, since $a_{k}=f_{k}$ . Take $h_{k}=x_{k+1}-x_{k}$ . The continuity condition (see P.R.Turner pg. 104) gives the following equalities:

$d_{k}=\frac{c_{k+1}-c_{k}}{3h_{k}}$
$b_{k}=\frac{f_{k+1}-f{k}}{h_{k}}-\frac{h_k}{3}(c_{k+1}+2c_k)$

Thus, if we had the values for $c_{k}$ , we would be able to determine all the coefficients. After some re-arranging, it is possible to obtain:

$h_{k}c_{k}+2(h_{k}+h_{k+1})c_{k+1}+h_{k+1}c_{k+2}=3(\frac{f_{k+2}-f_{k+1}}{h_{k+1}}-\frac{f_{k+1}-f_{k}}{h_k})$

for $k=0,1,...,n-3$ . This is a tridiagonal system of linear equations, which can be solved in a number of ways.

Let’s now look at how we can implement the linear and cubic spline interpolation in C#.

Implementing Linear and Cubic Spline Interpolation in C#

The code is broken into five regions. Tridiagonal Matrix region defines a Tridiagonal class to solve a system of linear equations. The Extensions regions defines a few extensions to allows for matrix manipulations. The Foundation region is where the parent Interpolation class is defined. Both, Linear and Cubic Spline Interpolations classes inherit from it.

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace TridiagonalMatrix
{
    #region TRIDIAGONAL_MATRIX

    // solves a Tridiagonal Matrix using Thomas algorithm
    public sealed class Tridiagonal
    {
        public double[] Solve(double[,] matrix, double[] d)
        {
            int rows = matrix.GetLength(0);
            int cols = matrix.GetLength(1);
            int len = d.Length;
            // this must be a square matrix
            if (rows == cols && rows == len)
            {

                double[] b = new double[rows];
                double[] a = new double[rows];
                double[] c = new double[rows];
               
                // decompose the matrix into its tri-diagonal components
                for (int i = 0; i < rows; i++)
                {
                    for (int j=0; j<cols; j++)
                    {
                        if (i == j)
                            b[i] = matrix[i, j];
                        else if (i == (j - 1))
                            c[i] = matrix[i, j];
                         else if (i == (j + 1))
                            a[i] = matrix[i, j];
                    }
                }
                try
                {
                    c[0] = c[0] / b[0];
                    d[0] = d[0] / b[0];

                    for (int i = 1; i < len - 1; i++)
                    {
                        c[i] = c[i] / (b[i] - a[i] * c[i - 1]);
                        d[i] = (d[i] - a[i] * d[i - 1]) / (b[i] - a[i] * c[i - 1]);
                    }
                    d[len - 1] = (d[len - 1] - a[len - 1] * d[len - 2]) / (b[len - 1] - a[len - 1] * c[len - 2]);

                    // back-substitution step
                    for (int i = (len - 1); i-- > 0; )
                    {
                        d[i] = d[i] - c[i] * d[i + 1];
                    }

                    return d;
                }
                catch(DivideByZeroException)
                {
                    Console.WriteLine("Division by zero was attempted. Most likely reason is that ");
                    Console.WriteLine("the tridiagonal matrix condition ||(b*i)||>||(a*i)+(c*i)|| is not satisified.");
                    return null;
                }
            }
            else
            {
                Console.WriteLine("Error: the matrix must be square. The vector must be the same size as the matrix length.");
                return null;
            }
        }
    }

    #endregion
}

namespace BasicInterpolation
{
    #region EXTENSIONS
    public static class Extensions
    {
        // returns a list sorted in ascending order 
        public static List<T> SortedList<T>(this T[] array)
        {
            List<T> l = array.ToList();
            l.Sort();
            return l;

        }

        // returns a difference between consecutive elements of an array
        public static double[] Diff(this double[] array)
        {
            int len = array.Length - 1;
            double[] diffsArray = new double[len];
            for (int i = 1; i <= len;i++)
            {
                diffsArray[i - 1] = array[i] - array[i - 1];
            }
                return diffsArray;
        }

        // scaled an array by another array of doubles
        public static double[] Scale(this double[] array, double[] scalor, bool mult=true)
        {
            int len = array.Length;
            double[] scaledArray = new double[len];
            
            if (mult)
            {
                for (int i = 0; i < len; i++)
                {
                    scaledArray[i] = array[i] * scalor[i];
                }
            }
            else
            {
                for (int i = 0; i < len; i++)
                {
                    if (scalor[i] != 0)
                    {
                        scaledArray[i] = array[i] / scalor[i];
                    }
                    else
                    {
                        // basic fix to prevent division by zero
                        scalor[i] = 0.00001;
                        scaledArray[i] = array[i] / scalor[i];

                    }
                }
            }

            return scaledArray;
        }

        public static double[,] Diag(this double[,] matrix, double[] diagVals)
        {
            int rows = matrix.GetLength(0);
            int cols = matrix.GetLength(1);
            // the matrix has to be scare
            if (rows==cols)
            {
              double[,] diagMatrix = new double[rows, cols];
              int k = 0;
              for (int i = 0; i < rows; i++)
                  for (int j = 0; j < cols; j++ )
                  {
                      if(i==j)
                      {
                          diagMatrix[i, j] = diagVals[k];
                          k++;
                      }
                      else
                      {
                          diagMatrix[i, j] = 0;
                      }
                  }
                      return diagMatrix;
            }
            else
            {
                Console.WriteLine("Diag should be used on square matrix only.");
                return null;
            }

            
        }
    }

    #endregion
    #region FOUNDATION
    internal interface IInterpolate
    {
        double? Interpolate( double p);
    }

    internal  abstract class Interpolation: IInterpolate
    {
        
        public Interpolation(double[] _x, double[] _y)
        {
            int xLength = _x.Length;
            if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength)
            {
                x = _x;
                y = _y;
            }
        }

        // cubic spline relies on the abscissa values to be sorted
        public Interpolation(double[] _x, double[] _y, bool checkSorted=true)
        {
            int xLength = _x.Length;
            if (checkSorted)
            {
                if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength && Enumerable.SequenceEqual(_x.SortedList(),_x.ToList()))
                {
                    x = _x;
                    y = _y;
                }
            }
            else
            {
                if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength)
                {
                    x = _x;
                    y = _y;
                }
            }
        }

        public double[] X
        {
            get
            {
                return x;
            }
        }

        public double[] Y
        {
            get
            {
                return y;
            }
        }

        public abstract double? Interpolate(double p);

        private double[] x;
        private double[] y;
    }

    #endregion

    #region LINEAR
    internal sealed class LinearInterpolation: Interpolation
    {
        
        public LinearInterpolation(double[] _x, double [] _y):base(_x,_y)
        {
            len = X.Length;
            if (len > 1)
            {
                Console.WriteLine("Successfully set abscissa and ordinate.");
                baseset = true;
                // make a copy of X as a list for later use
                lX = X.ToList();
            }
            else
                Console.WriteLine("Ensure x and y are the same length and have at least 2 elements. All x values must be unique.");
        }

        public override double? Interpolate(double p)
        {
            if (baseset)
            {
                double? result = null;
                double Rx;

                try
                {
                    // point p may be outside abscissa's range
                    // if it is, we return null
                    Rx = X.First(s => s >= p);
                }
                catch(ArgumentNullException)
                {
                    return null;
                }

                // at this stage we know that Rx contains a valid value
                // find the index of the value close to the point required to be interpolated for
                int i = lX.IndexOf(Rx);

                // provide for index not found and lower and upper tabulated bounds
                if (i==-1)
                    return null;
                        
                if (i== len-1 && X[i]==p)
                    return Y[len - 1];

                if (i == 0)
                    return Y[0];

                // linearly interpolate between two adjacent points
                double h = (X[i] - X[i - 1]);
                double A = (X[i] - p) / h;
                double B = (p - X[i - 1]) / h;

                result = Y[i - 1] * A + Y[i] * B;

                return result;
                
            }
            else
            {
                return null;
            }
        }

        private bool baseset = false;
        private int len;
        private List<double> lX;
    }

    #endregion

    #region  CUBIC_SPLINE
    internal sealed class CubicSplineInterpolation:Interpolation
    {
        public CubicSplineInterpolation(double[] _x, double[] _y): base(_x, _y, true)
        {
            len = X.Length;
            if (len > 1)
            {
               
                Console.WriteLine("Successfully set abscissa and ordinate.");
                baseset = true;
                // make a copy of X as a list for later use
                lX = X.ToList();
            }
            else
                Console.WriteLine("Ensure x and y are the same length and have at least 2 elements. All x values must be unique. X-values must be in ascending order.");
        }

        public override double? Interpolate(double p)
        {
            if (baseset)
            {
                double? result = 0;
                int N = len - 1;
                
                double[] h = X.Diff();
                double[] D = Y.Diff().Scale(h, false);
                double[] s = Enumerable.Repeat(3.0, D.Length).ToArray();
                double[] dD3 = D.Diff().Scale(s);
                double[] a = Y;
                
                // generate tridiagonal system
                double[,] H = new double[N-1, N-1];
                double[] diagVals = new double[N-1];
                for (int i=1; i<N;i++)
                {
                    diagVals[i-1] = 2 * (h[i-1] + h[i]);
                }

                H = H.Diag(diagVals);

                // H can be null if non-square matrix is passed
                if (H != null)
                {
                    for (int i = 0; i < N - 2; i++)
                    {
                        H[i, i + 1] = h[i + 1];
                        H[i + 1, i] = h[i + 1];
                    }

                    double[] c = new double[N + 2];
                    c = Enumerable.Repeat(0.0, N + 1).ToArray();

                    // solve tridiagonal matrix
                    TridiagonalMatrix.Tridiagonal le = new TridiagonalMatrix.Tridiagonal();
                    double[] solution = le.Solve(H, dD3);                   

                    for (int i = 1; i < N;i++ )
                    {
                        c[i] = solution[i - 1];
                    }

                    double[] b = new double[N];
                    double[] d = new double[N];
                    for (int i = 0; i < N; i++ )
                    {
                        b[i] = D[i] - (h[i] * (c[i + 1] + 2.0 * c[i])) / 3.0;
                        d[i] = (c[i + 1] - c[i]) / (3.0 * h[i]);
                    }

                    double Rx;
                    
                    try
                    {
                        // point p may be outside abscissa's range
                        // if it is, we return null
                        Rx = X.First(m => m >= p);
                    }
                    catch
                    {
                        return null;
                    }

                    // at this stage we know that Rx contains a valid value
                    // find the index of the value close to the point required to be interpolated for
                    int iRx = lX.IndexOf(Rx);

                    if (iRx == -1)
                        return null;

                    if (iRx == len - 1 && X[iRx] == p)
                        return Y[len - 1];

                    if (iRx == 0)
                        return Y[0];

                    iRx = lX.IndexOf(Rx)-1;
                    Rx = p - X[iRx];
                    result = a[iRx] + Rx * (b[iRx] + Rx * (c[iRx] + Rx * d[iRx]));

                        return result;
                }
                else
                {
                    return null;
                }

                
            }
            else
                return null;
        }

        private bool baseset = false;
        private int len;
        private List<double> lX;
    }
    #endregion
    class EntryPoint
    {
        static void Main(string[] args)
        {
            // code relies on abscissa values to be sorted
            // there is a check for this condition, but no fix
            // f(x) = 1/(1+x^2)*sin(x)
            double[] ex = { -5, -3, -2, -1, 0, 1, 2, 3, 5};
            double[] ey = { 0.036882, -0.01411, -0.18186, -0.42074, 0, 0.420735, 0.181859, 0.014112, -0.03688};
            double[] p = {-5,-4.5,-4,-3.5,-3.2,-3,-2.8,-2.1,-1.5,-1,-0.8,0,0.65,1,1.3,1.9,2.6,3.1,3.5,4,4.5,5 };

            LinearInterpolation LI = new LinearInterpolation(ex, ey);
            CubicSplineInterpolation CS = new CubicSplineInterpolation(ex, ey);

            Console.WriteLine("Linear Interpolation:");

            foreach (double pp in p)
            {
                Console.Write(LI.Interpolate(pp).ToString()+", ");

            }
            Console.WriteLine("Cubic Spline Interpolation:");
            foreach (double pp in p)
            {

                Console.WriteLine(CS.Interpolate(pp).ToString());
            }
            Console.ReadLine();
        }
    }
}

Note that I wrote a console application, and this is the reason for throwing as few exceptions as possible. Like with all the code on my blog – please feel free to take it and modify as you wish. It is now time to compare performance of linear and cubic spline interpolations on a test function: $f(x)=\frac{1}{1+x^{2}}\sin x$ . Using the above code we obtain the following results:

Decision Tree Classifier – Part 1

On March 9, 2015September 1, 2016 By ElenaIn Machine Learning, Numerical Analysis

To continue my blogging on machine learning (ML) classifiers, I am turning to decision trees. The post on decision trees will be in two parts. Part 1 will provide an introduction to how decision trees work and how they are build. Part 2 will contain the C# implementation of an example decision trees classifier. As in all my posts, I prefer clear and informal explanation over the terse mathematical one. So, any pedants out there – look away now!

Decision trees are a great choice for inductive inference and have been widely used for a long time in the field of Artificial Intelligence (AI). In this post we will cover the decision tree algorithm known as ID3.
There are several reasons why decision trees are great classifiers:

decision trees are easy to understand;
decision trees work well with messy data or missing values;
decision trees give insight into complex data;
decision trees can be visualized to allow for inference inspection or correction;
decision tree building algorithms can be as simple or sophisticated as required (e.g. they can incorporate pruning, weights, etc.);

Decision trees work best with discrete classes. That is, the output class for each instance is either a string, boolean or an integer. If you are working with continuous values, you may consider rounding and mapping to a discrete output class, or may need to look for another classifier. Decision trees are used for classification problems. For example, the taxonomy of organisms, plants, minerals, etc. lends itself naturally to decision tree classifiers. This is because in a field of taxonomy we are dealing with a set of records containing values for some attributes. The values come from a finite set of known features. Each record may or may not have a classification. Medicine is another field that makes use of decision trees. Almost all illnesses can be categorized by symptoms, thus decision trees aid doctors in illness diagnosis.

It is time for an example, which I am borrowing from [1]. The tennis playing example in ML is like the ‘Hello World’ in programming languages. We are given some data about the weather conditions that are appropriate for playing tennis. Our task is to construct a decision tree based on this data, and use the tree to classify unknown weather conditions. The learning data is:

Table 1
Outlook	Temperature	Humidity	Wind	Play Tennis
sunny	hot	high	strong	no
sunny	hot	high	weak	no
overcast	hot	high	weak	yes
rain	mild	high	weak	yes
rain	cool	normal	weak	yes
rain	cool	normal	strong	no
overcast	cool	normal	strong	yes
sunny	mild	high	weak	no
sunny	cool	normal	weak	yes
rain	mild	normal	weak	yes
sunny	mild	normal	strong	yes
overcast	mild	high	strong	yes
overcast	hot	normal	weak	yes
rain	mild	high	strong	no

Table 1 tells us which weather conditions are good for playing tennis outdoors. For example, if it is sunny, and the wind is weak, and the temperature is mild but it is very humid, then playing tennis outdoors is not advisable. On the other hand, on an overcast day, regardless of the wind, playing tennis outdoors should be OK.

The most fundamental concept behind the decision tree classifiers is that of order. The amount of order in the data can be measured by assessing its consistency. For example, imagine that every row in Table 1 had a ‘yes’ associated with the Play Tennis column. This would tell us that regardless of the wind, temperature, humidity, we can always play tennis outside. The data would have perfect order, and we would be able to build a perfect classifier for the data – the one that always says ‘yes’ and is always correct. The other extreme would be where the outcome class differs for every observation. For an inductive learner like a decision tree, this would mean that it is impossible to classify new instance unless it perfectly matches some instance in the training set. This is why decision tree classifier won’t work for continuous class problems.

In information theory the concept of order (actually, lack of it), is often represented by entropy. It is a scary word for something that is rather simple. Entropy definition was proposed by the founder of information theory – Claude Shannon, and it is a probabilistic measure of categorical data defined as:

$Entropy(S) = -\sum_{i=1}^{n}p_i \log_2 p_i$

where S is the training data set with some target classification that takes on n different values. The discrete target values are assigned their probabilities p, and $\log_2$ is logarithm base 2. The base two is due to the entropy being a measure of the expected encoding in binary format (i.e. 0s and 1s). Note that the smaller are individual probabilities, the greater is the absolute value of entropy. Also, the closer is entropy to zero, the more order there is in the data.

We now can calculate the entropy of our data, one column at a time. Let’s take the Play Tennis column. We have 9 ‘yes’ and 5 ‘no’, this gives us the entropy of $Entropy(S)=-\frac{9}{14} \log_2(\frac{9}{14}) + -\frac{5}{14}\log_2(\frac{5}{14})=0.940$ , accurate to 3 d.p. There is a reason why we started with the class column. It will be used to measure the information gain we can achieve by splitting the data one attribute/column at a time, which is the core idea behind building decision trees. At each step we will be picking the attribute that achieves the greatest information gain to split the tree recursively. The information gain is, essentially, a positive difference in entropy; and the root node of any decision tree is the attribute with the greatest information gain. Information gain is formally defined as:

$InfoGain(S,A) = Entropy(S) -\sum_{i=1}^{A}\frac{|S_i|}{|S|}Entropy(S_i)$

where A is the set of all values some attribute takes. For example, the Wind column takes values in {strong, weak}, and the Humidity column takes on values in {high, normal}. $|S_i|$ and $|S|$ are the number of records taking on the value i and the total number of records respectively. Finally, $Entropy(S_i)$ is the corresponding entropy of all records where the attribute A takes on value i with respect to the target class. The last sentence is important. It means that, given all the records where attribute A takes on the same value i we are interested to know the dispersion of the target class. For example, take a look at all the records where Wind is strong. Here we have 3 records where the target class is ‘no’ and 3 records where it is ‘yes’. Thus, the corresponding entropy is $Entropy(S_{wind=strong})=-\frac{3}{6} \log_2(\frac{3}{6}) -\frac{3}{6} \log_2(\frac{3}{6})=1.0$

So, which attribute/column should be the tree’s root node? It should be the one that achieves the greatest information gain:

$InfoGain(S,Wind) = 0.940 - \frac{8}{14}\times 0.811 - \frac{6}{14}\times 1.0=0.048$
$InfoGain(S,Humidity) = 0.940 - \frac{7}{14}\times 0.985 - \frac{7}{14}\times 0.592=0.151$
$InfoGain(S,Temperature) = 0.940 - \frac{4}{14}\times 1.0 - \frac{4}{14}\times 0.811 - \frac{6}{14}\times 0.918=0.029$
$InfoGain(S,Outlook) = 0.940 - \frac{5}{14}\times 0.971 - \frac{4}{14}\times 0.0 - \frac{5}{14}\times 0.971=0.246$

It is clear that Outlook achieves the greatest information gain and should be the root of the tree. The worst information gain would be achieved with Temperature attribute. This is what our tree now looks:

At this stage we have the training data split into three clusters. Where outlook is overcast, we have a target class of ‘yes’. We now proceed recursively building the sub-tree in the other two clusters. Where outlook is sunny, we have a total of 5 records. These are reproduced in Table 2 below. Out of three possible attributes for the node we again pick the one that achieves the greatest information gain. If you inspect the data in Table 2, it is easy to see that humidity is that attribute since all five records can be split as following: if humidity is normal, then ‘yes’, else ‘no’. Its corresponding information gain is

$InfoGain(S_{sunny},Humidity) = 0.970 - \frac{3}{5}\times 0 - \frac{2}{5}\times 0=0.970$

where 0.970 is entropy of Outlook is sunny, again, with respect to the Play Tennis class: $Entropy(S_{sunny}) = - \frac{3}{5}\log_2(\frac{3}{5})- \frac{2}{5}\log_2(\frac{2}{5})=0.970$ .

Table 2
Outlook	Temperature	Humidity	Wind	Play Tennis
sunny	hot	high	strong	no
sunny	hot	high	weak	no
sunny	mild	high	weak	no
sunny	cool	normal	weak	yes
sunny	mild	normal	strong	yes

At this stage we have classified 9 records and our tree has 9 terminal descendant nodes (leaves):

We can now deal with the records in the last outlook cluster, i.e. where outlook is rain. Here we have five records, which are reproduced below in Table 3:

Table 3
Outlook	Temperature	Humidity	Wind	Play Tennis
rain	mild	high	weak	yes
rain	cool	normal	weak	yes
rain	cool	normal	strong	no
rain	mild	normal	weak	yes
rain	mild	high	strong	no

We apply the same algorithm as before by selecting the attribute for the next node that gives the greatest information gain. It is easy to spot that the Wind attribute achieves just that. Its total information gain is

$InfoGain(S_{rain},Wind) = 0.970 - \frac{3}{5}\times 0 - \frac{2}{5}\times 0=0.970$

The complete tree looks like this:

A few things should be noted about the final decision tree. Firstly, the Temperature attribute is completely missing. The constructed decision tree allowed us to see that this attribute is redundant, at least given the training dataset. Decision trees always favor the shorter trees over the longer ones, which is the main part of its inductive bias (or the algorithm’s policy). Secondly, this is not a binary tree, since we have parent nodes with more than two edges (i.e. the Outlook node). Finally, the constructed decision tree allows for a one-way searching algorithm. This means that we cannot back-track to the parent node. In the grand scheme of things this implies that a decision tree can end up at a locally optimal, rather than globally optimal solution.

The next blog post will be on how to implement the decision tree classifier in C#.

References:

[1]. T.M.Mitchell. Machine Learning. McGraw-Hill. 1997.

k Nearest Neighbor Classifier

On March 3, 2015September 1, 2016 By ElenaIn Machine Learning, Numerical Analysis

On my blog space I am going to share with you example implementations of the most common machine learning techniques. The code will be either in C# or Python.

This is the first post in the series of several posts to come, which will be on algorithms commonly used to implement classifiers. A classifier is a machine learning algorithm that is allowed to build a representation of data on some training dataset, and ultimately is used to classify new unobserved instances. Classifiers are at the heart of machine learning and data mining, and they have wide use in medicine, speech and image recognition, and even finance. Broadly speaking all classifier fall into two categories: supervised and unsupervised. Supervised classifiers need to be ‘trained’, in the sense that they are fed the training data with known classifications, which is used to construct the priory. Unsupervised classifiers are a bit more complex, and work with unlabeled/unclassified training data (e.g. k-means clusters) or even have to learn the target class for each instance by trial and error (e.g. reinforced learning).

We’ll begin by looking at the most basic instance based classifier known as the K-Nearest Neighbour (kNN). Here K is the number of instances used to cast the vote when labeling previously unobserved instance. To demonstrate how kNN works, we will take this example dataset:

Table 1
Attr 1	Attr 2	Attr 3	Class
0.7	10	300	A
0.14	9	120	A
1.0	12	200	B
1.12	15	300	B
0.4	7	150	A
0.6	8	600	A
1.15	15	600	B
1.12	11	400	B

The above is a dataset with four columns and eight rows. The first three columns are the data (numerical format is required for kNN), the last column is the class. For the purpose of this example it does not matter what the data represents. I created random example with a hidden pattern, which, hopefully, our kNN algorithm can recognise.

Given previously unobserved instance I={i0,…,iN,class}, we calculate the Euclidean distance between I and each known instance in the dataset as follows:

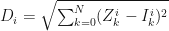
$D_i= \sqrt{\sum_{k=0}^{N}(Z^{i}_{k}-I^{i}_{k})^2}$

Here Z is a sequence of values of some instance i in attribute k for which a classification is given (see the dataset), and I is the unclassified instance.
For example, given I = {Attr1=12, Attr2=11, Attr3=500}, the resulting distance matrix, after normalisation, is the following:

Table 2
D	Class
11.196	A
11.772	A
10.909	B
10.792	B
11.519	A
11.295	A
10.756	B
10.774	B

The distances were calculated on normalised data. That is, instead of using the original values in Table 1, where the 3rd column dominates all other values, we normalise each value according to:

$\frac{Z_{k}^{i}-Min(Z_{k})}{Max(Z_{k})-Min(Z_{k})}$

Again, Z is from the dataset. The instance that we need to classify is also normalised. For example, the normalised values for Table 1 are:

Table 3
Attr 1	Attr 2	Attr 3	Class
0.554	0.375	0.375	A
0	0.25	0	A
0.851	0.625	0.167	B
0.970	1	0.375	B
0.257	0	0.062	A
0.455	0.125	1	A
1	1	1	B
0.970	0.5	0.583	B

The normalised I = {11.74, 0.5, 0.792}, which was calculated with max and min from the dataset, excluding the instance we need to classify.

Ok, now that we have calculated the distances (Table 2), we can proceed to vote on which class the instance I should belong to. To do this, we select K smallest distances and look at their corresponding classes. Let’s take K=3, then the smallest distances with votes are: 10.756 for B, 10.774 for B, and 10.792 for B. The new instance clearly belongs to class B. This is spot on, as the pattern is: Attr1<1 and Attr2<10 result in A, else B.

Consider another example I = {0.8, 11, 500}. For this instance, after normalisation, the top 3 distances with classes are: 0.379 for B, 0.446 for A, and 0.472 for A. The majority is A, so, the instance is classified as A.

Several modifications exist to the basic kNN algorithm. Some employ weights to improve classification, others use an even K and break ties in a weighted-fashion. Overall, it is a powerful, easy to implement classifier. If you are dealing with non-numeric data parameters, these can be quantified through some mapping from non-numeric value to numbers. Always remember to normalise your data, otherwise you are running a chance of introducing bias into the classifier.

Let’s now look at how kNN can be implemented with C#. At the start, I introduce several extensions to aid in data manipulation. In C#, extensions are an extremely useful concept and are quite addictive. And so is LINQ. You will notice that I try to use LINQ query where possible. Most worker method are private and my properties are read-only. Another thing to note is that my kNN constructor is private. Instead, the class users call initialiseKNN method which ensures that K is odd, since I am not using weights and don’t provide for tie breaks.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;

namespace kNN
{
    //extension method to aid in algorithm implementation
    public static class Extensions
    {
        //converts string representation of number to a double
        public static IEnumerable<double> ConvertToDouble<T>(this IEnumerable<T> array)
        {
            dynamic ds;
            foreach (object st in array)
            {
                ds = st;
                yield return Convert.ToDouble(ds);
            }
        }

        //returns a row in a 2D array
        public static T[] Row<T>(this T[,] array, int r)
        {
            T[] output = new T[array.GetLength(1)];
            if (r < array.GetLength(0))
            {
                for (int i = 0; i < array.GetLength(1); i++)
                    output[i] = array[r, i];
            }
            return output;
        }

        //converts a List of Lists to a 2D matrix
        public static T[,] ToMatrix<T>(this IEnumerable<List<T>> collection, int depth, int length)
        {
            T[,] output = new T[depth, length];
            int i = 0, j = 0;
            foreach (var list in collection)
            {
                foreach (var val in list)
                {
                    output[i, j] = val;
                    j++;
                }
                i++; j = 0;
            }

            return output;
        }

        //returns the classification that appears most frequently in the array of classifications
        public static string Majority<T>(this T[] array)
        {
            if (array.Length > 0)
            {
                int unique = array.Distinct().Count();
                if (unique == 1)
                    return array[0].ToString();

                return (from item in array
                             group item by item into g
                             orderby g.Count() descending
                             select g.Key).First().ToString();
            }
            else
                return "";
        }
    }

    /// <summary>
    /// kNN class implements the K Nearest Neighbor instance based classifier
    /// </summary>
    public sealed class kNN
    {
        //private constructor allows to ensure k is odd
        private  kNN(int K, string FileName, bool Normalise)
        {
            k = K;
            PopulateDataSetFromFile(FileName, Normalise);
        }

        /// <summary>
        /// Initialises the kNN class, the observations data set and the number of neighbors to use in voting when classifying
        /// </summary>
        /// <param name="K">integer representiong the number of neighbors to use in the classifying instances</param>
        /// <param name="FileName">string file name containing knows numeric observations with string classes</param>
        /// <param name="Normalise">boolean flag for normalising the data set</param>
        public static kNN initialiseKNN(int K, string FileName, bool Normalise)
        {
            if (K % 2 > 0)
                return new kNN(K, FileName, Normalise);
            else
            {
                Console.WriteLine("K must be odd.");
                return null;
            }
        }

        //read-only properties
        internal int K { get { return k; } }
        internal Dictionary<List<double>, string> DataSet { get { return dataSet;} }

        /// <summary>
        /// Classifies the instance according to a kNN algorithm
        /// calculates Eucledian distance between the instance and the know data
        /// </summary>
        /// <param name="instance">List of doubles representing the instance values</param>
        /// <returns>returns string - classification</returns>
        internal string Classify(List<double> instance)
        {
            int i=0;
            double [] normalisedInstance = new double[length];

            if (instance.Count!=length)
            {
                return "Wrong number of instance parameters.";
            }

            if (normalised)
            {
                foreach (var one in instance)
                {
                    normalisedInstance[i] = (one - originalStatsMin.ElementAt(i)) / (originalStatsMax.ElementAt(i) - originalStatsMin.ElementAt(i));
                    i++;
                }
            }
            else
            {
                normalisedInstance = instance.ToArray();
            }

            double[,] keyValue = dataSet.Keys.ToMatrix(depth, length);
            double[] distances = new double[depth];

            Dictionary<double, string> distDictionary = new Dictionary<double, string>();
            for (i = 0; i < depth; i++)
            {
                distances[i] = Math.Sqrt(keyValue.Row(i).Zip(normalisedInstance, (one, two) => (one - two) * (one - two)).ToArray().Sum());
                distDictionary.Add(distances[i], dataSet.Values.ToArray()[i]);

            }

            //select top votes
            var topK = (from d in distDictionary.Keys
                        orderby d ascending
                        select d).Take(k).ToArray();

            //obtain the corresponding classifications for the top votes
            var result = (from d in distDictionary
                        from t in topK
                        where d.Key==t
                        select d.Value).ToArray();

            return result.Majority();
        }
        /// <summary>
        /// Processess the file with the comma separated training data and populates the dictionary
        /// all values except for the class must be numeric
        /// the class is the last element in the dataset for each record
        /// </summary>
        /// <param name="fileName">string fileName - the name of the file with the training data</param>
        /// <param name="normalise">bool normalise - true if the data needs to be normalised, false otherwiese</param>
        private void PopulateDataSetFromFile(string fileName, bool normalise)
        {
            using (StreamReader sr = new StreamReader(fileName,true))
            {
                List<string> allItems = sr.ReadToEnd().TrimEnd().Split('\n').ToList();

                if (allItems.Count > 1)
                {
                    string[] array = allItems.ElementAt(0).Split(',');
                    length = array.Length - 1;
                    foreach (string item in allItems)
                    {
                        array = item.Split(',');
                        dataSet.Add(array.Where(p => p != array.Last()).ConvertToDouble().ToList(), array.Last().ToString().TrimEnd());
                    }
                    array = null;
                }
                else
                    Console.WriteLine("No items in the data set");
            }
            if (normalise)
            {
                NormaliseDataSet();
                normalised = true;
            }
        }

        private void NormaliseDataSet()
        {
            var keyCollection = from n in dataSet.Keys
                                select n;
            var valuesCollection = from n in dataSet.Values
                                   select n;

            depth = dataSet.Keys.Count;
            double[,] transpose = new double[length, depth];
            double[,] original = new double[depth, length];
            int i = 0, j = 0;

            //transpose
            foreach (var keyList in keyCollection)
            {
                foreach (var key in keyList)
                {
                    transpose[i, j] = key;
                    i++;
                }
                j++; i = 0;
            }

            //normalise
            double max, min;

            for (i = 0; i < length; i++)
            {
                originalStatsMax.Add (max = transpose.Row(i).Max());
                originalStatsMin.Add(min = transpose.Row(i).Min());

                for (j = 0; j < depth; j++)
                {
                    transpose[i, j] = (transpose[i, j] - min) / (max - min);
                }

            }
            for (i = 0; i < depth; i++)
            {
                for (j = 0; j < length; j++)
                    original[i, j] = transpose[j, i];
            }

            //overwrite the current values with the normalised ones
            dataSet = new Dictionary<List<double>, string>();
            for (i = 0; i < depth; i++)
            {
                dataSet.Add(original.Row(i).ToList(), valuesCollection.ElementAt(i));
            }
        }

        //private members
        private Dictionary<List<double>, string> dataSet = new Dictionary<List<double>,string>();
        private List<double> originalStatsMin = new List<double>();
        private List<double> originalStatsMax = new List<double>();
        private int k=0;
        private int length=0;
        private int depth=0;
        private bool normalised = false;
    }

    class EntryPoint
    {
        static void Main(string[] args)
        {
            kNN examplekNN = kNN.initialiseKNN(3,"DataSet.txt",true);

            List<double> instance2Classify = new List<double> {12,11,500};
            string result = examplekNN.Classify(instance2Classify);
            Console.WriteLine("This instance is classified as: {0}", result);
            Console.ReadLine();
        }
    }
}

In my next blog we will look at decision trees – a slightly more complicated, but also more powerful machine learning algorithm.

Transforming Uniform Random Variables to Normal

On February 25, 2015February 26, 2015 By ElenaIn Monte Carlo

In my previous post here I have shared with you some methods for generating uniform random variables. For many practical tasks we need random variables that are distributed normally around some mean. There are two well know approaches for transforming uniform random variables to normal or Gaussian. These are – the inverse transform and the Box-Muller methods. Let’s take a look at each of them. I am also providing my version of C# implementation.

Inverse Transform Method

The general form of this method is:

$X=F^{-1} (U),U\approx Unif[0,1]$

Here U is a uniform random variable from [0,1] interval, $F^{-1}$ is the inverse of the cumulative distribution function (i.e. any given c.d.f.), and X is the desired random variable satisfying $P(X \leq x)=F(x)$ property. Again, the c.d.f. can be for any required distribution for which the inverse is well-defined.

To make sense of this method and to see why it works, let’s take a look at the graph of a normal c.d.f. where $X \approx N(0,1)$ . Figure 1 shows the probability on the y-axis and the random variable on the x-axis. The probability axis corresponds to the uniform random variable range, which is [0,1]. Thus, we can use the y-axis to map to the x-axis, which would give us a random variable in (-3,3) interval. This random variable is normally distributed with mean 0 and standard deviation of 1. In Figure 1 I have marked the middle of both axis to make it clear that uniform random variables between 0 and 0.5 would map to normal random variables that are negative. The uniforms above 0.5 map to positive r.vs.

I hope by now it is clear how the inverse transform method works. The main reason it always works for a well-behaved distribution like the normal distribution is because the ‘mapping’ is one-to-one. That is, for each value of U, we have a unique mapping onto X. A good intuitive way to think about the inverse transform method is by analogy to taking a percentile of some distribution.

The standard normal cumulative distribution function is:

$F(x)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} \exp{\frac{-u^{2}}{2}} du$

To use the inverse transform method we need to take the inverse, or calculate $F^{-1}$ , for which an exact solution is not achievable computationally, and we will need to approximate it. Several numerical approximations can be found in the relevant literature. Check out, for example chapter 2.3.2 in [1] or on the Wikipedea. I will demonstrate two approximations of two different levels of accuracy.

In [1] we find a summary of the rational approximation proposed by Beasley and Springer:

$F^{-1} (x) \approx \frac{\sum_{n=0}^{3} a_n (x-\frac{1}{2})^{(2n+1)}}{1+\sum_{n=0}^{3} b_n (x-\frac{1}{2})^{2n}}$

Where $a_n$ and $b_n$ are constants (see the code for their values). The above is defined for $0.5 \le x \le0.92$ . For $x > 0.92$ , we can utilize Chebyshev’s approximation, as demonstrated in [1]:

$F^{-1} (x) \approx \sum_{n=0}^{8} c_n (\log(-\log(1-x)))^{n} ,0.92 \leq x<1$

The values below 0.5 can be derived by symmetry. The above method gives a high accuracy with a maximum absolute error of $3*10^{-9}$ over the [-7,7] range for x.

A less accurate method involves approximating the error function erf, since the inverse c.d.f. can be defined in terms of erf as follows:

$F^{-1} (x)=\sqrt{2} \cdot erf^{-1} (2x-1)$

The inverse error function can be approximated using:

$erf^{-1} (x) \approx sign(x) \sqrt{\theta}$

$\theta =\sqrt{{\left(\frac{2}{\pi\alpha}+\frac{ln(1-x^{2})}{2}\right)}^{2}-\frac{ln(1-x^{2})}{\alpha}}-\frac{2}{\pi\alpha}+\frac{ln(1-x^{2})}{2}$

$\alpha =\frac{8(\pi-3)}{3\pi(4-\pi)}$

This approach achieves a maximum absolute error of 0.00035 for all x. To me, the erf method is simpler, both, to understand and to implement.

Box-Muller Method

Box-Muller method for transforming uniform random variables to normal r.vs. is an algorithms that involves choosing a random point uniformly from the circle of radius $\sqrt{R}$ , such that $R=Z_1^{2}+Z_2^{2}$ follows exponential distribution with mean 2 and $Z_n\sim N_2 (0,I_2 )$ (i.e. bivariate normal).

Box-Muller method requires two uniform random variables, and it produces two standard normal random variables. The reason for having two, is because we are simulating a point on a circle in x,y plane. So, to pick a random point on a circle we need a radius and the angle it makes with the origin. If we can randomise the radius and the angle with the origin (using the two random uniforms), we can achieve a random way of simulating the (x,y) point on a circle. Take a look at Figure 2 below, which demonstrates this concept.

Ok, hopefully the above gives you a clear explanation for the foundations of the inverse transform and the Box-Muller methods. Let’s now look at how we can implement them in C#.

Implementation

Box-Muller class has an overloaded method that works for a single pair or a 2D array of r.v.s:

internal sealed class BoxMuller
    {
        /// <summary>
        /// Returns an arrays with Z1 and Z2 - two standard normal random variables generated using Box-Muller method
        /// </summary>
        /// <param name="U1">first standard random uniform</param>
        /// <param name="U2">second standard randoom uniform</param>
        /// <returns>double[] of length=2</returns>
        internal double[] BoxMullerTransform(double U1, double U2)
        {
            double[] normals = new double[2];
            if (U1 < 0 || U1 > 1 || U2 < 0 || U2 > 1)
            {
                normals[0] = default(double);
                normals[1] = default(double);
            }
            else
            {
                double sqrtR = Math.Sqrt(-2.0*Math.Log(U1));
                double v = 2.0*Math.PI*U2;

                normals[0] = sqrtR * Math.Cos(v);
                normals[1] = sqrtR * Math.Sin(v);
            }
            return normals;
        }

        /// <summary>
        /// Returns a 2D array with Z1[] and Z2[] - two standard normal random variables generated using Box-Muller method
        /// </summary>
        /// <param name="U1">u1[] an array of first standard random uniforms</param>
        /// <param name="U2">u2[] an array of second standard random uniforms</param>
        /// <returns>double[L,2] of L=min(Length(u1),Length(u2))</returns>
        internal double[,] BoxMullerTransform(double[] U1, double[] U2)
        {
            long count=U1.Length<=U2.Length?U1.Length:U2.Length;

            double[,] normals = new double[count, 2];
            double u1, u2;

            for (int i = 0; i < count; i++)
            {
                u1 = U1[i];
                u2 = U2[i];
                if (u1 < 0 || u1 > 1 || u2 < 0 || u2 > 1)
                {
                    normals[i,0] = default(double);
                    normals[i,1] = default(double);
                }
                else
                {
                    double sqrtR = Math.Sqrt(-2.0 * Math.Log(u1));
                    double v = 2.0 * Math.PI * u2;

                    normals[i,0] = sqrtR * Math.Cos(v);
                    normals[i,1] = sqrtR * Math.Sin(v);
                }
            }
            return normals;
        }
    }

The inverse transform has four internal methods for generating normal r.v.s. As described before, the ERF method is simpler, and is also easier to implement. The Beasley-Springer-Moro (BSM) method is based on the algorithm found in [1], pg. 68. I’ve verified that it gives an accurate solution up to 9.d.p. Note that InverseTransformERF is an approximation to InverseTransformMethod, and it seems to achieve an accuracy of up to 4 d.p.

internal sealed class InverseTransform
    {
        /// <summary>
        /// Returns a standard normal random variable given a standard uniform random variable
        /// </summary>
        /// <param name="x">standard uniform rv in [0,1]</param>
        /// <returns>standard normal rv in (-3,3)</returns>
        internal double InverseTransformMethod(double x)
        {
            if (x < 0 || x > 1)
                return default(double);
            
            double res,r;
            double y = x - 0.5;
            if(y<0.42)
            {
                r = y * y;
                res = y * (((a3 * r + a2) * r + a1) * r + a0) / ((((b3 * r + b2) * r + b1) * r + b0) * r + 1.0);
            }
            else
            {
                r = (y > 0) ? (1 - x) : x;
                r = Math.Log(-1.0 * Math.Log(r));
                res = c0 + r * (c1 + r * (c2 + r * (c3 + r * (c4 + r * (c5 + r * (c6 + r * c7 + r * c8))))));
                res = (y < 0) ? -1.0 * res : res;
            }
            return res;
        }
        /// <summary>
        /// Returns an array of standard normal random variables given an array of standard uniform random variables
        /// </summary>
        /// <param name="x">an array of doubles: uniform rvs in [0,1]</param>
        /// <returns>an array of doubles: standard normal rvs in (-3,3)</returns>
        internal double[] InverseTransformMethod(double[] x)
        {
            long size = x.Length;
            double[] res = new double[size];
            double r,y;


            for (int i = 0; i < size;i++)
            {
                if (x[i]<0 || x[i]>1)
                {
                    res[i] = 0;
                    continue;
                }

                y = x[i] - 0.5;
                if (y < 0.42)
                {
                    r = y * y;
                    res[i] = y * (((a3 * r + a2) * r + a1) * r + a0) / ((((b3 * r + b2) * r + b1) * r + b0) * r + 1.0);
                }
                else
                {
                    r = (y > 0) ? (1 - x[i]) : x[i];
                    r = Math.Log(-1.0 * Math.Log(r));
                    res[i] = c0 + r * (c1 + r * (c2 + r * (c3 + r * (c4 + r * (c5 + r * (c6 + r * c7 + r * c8))))));
                    res[i] = (y < 0) ? -1.0 * res[i] : res[i];
                }
            }
            return res;
        }
        /// <summary>
        /// Performs an inverse transform using erf^-1
        /// Returns a standard normal random variable given a standard uniform random variable
        /// </summary>
        /// <param name="x">standard uniform rv in [0,1]</param>
        /// <returns>standard normal rv in (-3,3)</returns>
        internal double InverseTransformERF(double x)
        {
            return Math.Sqrt(2.0) * InverseErf(2.0 * x - 1);
        }

        /// <summary>
        /// Performs an inverse transform using erf^-1
        /// Returns an array of standard normal random variables given an array of standard uniform random variables
        /// </summary>
        /// <param name="x">an array of doubles: uniform rvs in [0,1]</param>
        /// <returns>an array of doubles: standard normal rvs in (-3,3)</returns>
        internal double[] InverseTransformERF(double[] x)
        {
            long size = x.Length;
            double[] res = new double[size];
            for (int i = 0; i < size; i++ )
            {
                res[i] = Math.Sqrt(2.0) * InverseErf(2.0 * x[i] - 1);
            }
                return res;
        }

        private double InverseErf(double x)
        {
            double res;
            double K = scalor + (Math.Log(1 - x * x)) / (2.0);
            double L=(Math.Log(1-x*x))/(alpha);
            double T = Math.Sqrt(K*K - L);

            res = Math.Sign(x) * Math.Sqrt(T-K);
            return res;
        }

        //used by the ERF method
        private const double alpha = (8.0 * (Math.PI - 3.0)) / (3.0 * Math.PI * (4.0 - Math.PI));
        private const double scalor = (2.0) / (Math.PI * alpha);

        //used by the BSM method in "Monte Carlo Methods in Financial Engineering" by P.Glasserman
        //note that a double achieves 15-17 digit precision
        //since these constancts are small, we are not using decimal type
        private const double a0 = 2.50662823884;
        private const double a1 = -18.61500062529;
        private const double a2 = 41.39119773534;
        private const double a3 = -25.44106049637;
        private const double b0 = -8.47351093090;
        private const double b1 = 23.08336743743;
        private const double b2 = -21.06224101826;
        private const double b3 = 3.13082909833;
        private const double c0 = 0.3374754822726147;
        private const double c1 = 0.9761690190917186;
        private const double c2 = 0.16079797149118209;
        private const double c3 = 0.0276438810333863;
        private const double c4 = 0.0038405729373609;
        private const double c5 = 0.0003951896511919;
        private const double c6 = 0.0000321767881768;
        private const double c7 = 0.0000002888167364;
        private const double c8 = 0.0000003960315187;

    }

Surely the two different methods map the uniforms to different normal r.v.s. So, how can we compare these two methods? One way would be to consider simplicity, speed and the accuracy vs. the exact solution.

References:
[1]P. Glasserman. “Monte Carlo Methods in Financial Engineering”, 2004. Springer-Verlag.

codefying

Tag: Numerical Analysis

Computing Bond Yield with Newton’s Method

The Newton’s Method

Goal Seek in C#

Linear and Cubic Spline Interpolation

Linear Interpolation

Cubic Spline Interpolation

Implementing Linear and Cubic Spline Interpolation in C#

Decision Tree Classifier – Part 1

k Nearest Neighbor Classifier

Transforming Uniform Random Variables to Normal

Inverse Transform Method

Box-Muller Method

Implementation

The Newton’s Method

Goal Seek in C#

Share this:

Linear Interpolation

Cubic Spline Interpolation

Implementing Linear and Cubic Spline Interpolation in C#

Share this:

Share this:

Inverse Transform Method

Box-Muller Method

Implementation

Share this: