In this post on numerical methods I will share with you the theoretical background and the implementation of the two types of interpolations: linear and natural cubic spline. These interpolations are often used within the financial industry. For example, discount rates for some maturity for which there is no point on an yield curve is often interpolated using cubic spline interpolation. Another example can be in risk management, like a position’s Value-at-Risk calculation obtained from a partial or a 2-dimensional revaluation grid.
Linear Interpolation
Let’s begin with the simplest method – linear interpolation. The idea is that we are given a set of numerical points and function values at these points. The task is to use the given set and approximate the function’s value at some different points. That is, given 
Almost all interpolation techniques are based around the concept of function approximation. Mathematically, the backbone is simple:
The above expression tells us that the value of the function we are approximating at point x will be around 
where we have substituted 
Linear interpolation is the most basic type of interpolations. It works remarkably well for smooth functions with sufficient number of points. However, because it is such a basic method, interpolating more complex functions requires a little bit more work.
Cubic Spline Interpolation
In what follows I am going to borrow a few formulations from a very good book: Guide to Scientific Computing by P.R.Turner. The idea of a spline interpolation is to extend the single polynomial of linear interpolation to higher degrees. But unlike with piece-wise polynomials, the higher degree polynomials constructed by the cubic spline are different in each interval ![[x_i, x_{i+1}]](https://s0.wp.com/latex.php?latex=%5Bx_i%2C+x_%7Bi%2B1%7D%5D&bg=ffffff&fg=111111&s=0&c=20201002)
If you compare the above expression with the linear interpolation, you will see that we have added two terms to the rhs. It is these extra terms that should allow us achieve greater precision. There are certain requirements placed on s. These are: it must be continuous, and its first and second derivatives must exist. We only need to determine 
Thus, if we had the values for 
for 
Let’s now look at how we can implement the linear and cubic spline interpolation in C#.
Implementing Linear and Cubic Spline Interpolation in C#
The code is broken into five regions. Tridiagonal Matrix region defines a Tridiagonal class to solve a system of linear equations. The Extensions regions defines a few extensions to allows for matrix manipulations. The Foundation region is where the parent Interpolation class is defined. Both, Linear and Cubic Spline Interpolations classes inherit from it.
using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace TridiagonalMatrix
{
#region TRIDIAGONAL_MATRIX
// solves a Tridiagonal Matrix using Thomas algorithm
public sealed class Tridiagonal
{
public double[] Solve(double[,] matrix, double[] d)
{
int rows = matrix.GetLength(0);
int cols = matrix.GetLength(1);
int len = d.Length;
// this must be a square matrix
if (rows == cols && rows == len)
{
double[] b = new double[rows];
double[] a = new double[rows];
double[] c = new double[rows];
// decompose the matrix into its tri-diagonal components
for (int i = 0; i < rows; i++)
{
for (int j=0; j<cols; j++)
{
if (i == j)
b[i] = matrix[i, j];
else if (i == (j - 1))
c[i] = matrix[i, j];
else if (i == (j + 1))
a[i] = matrix[i, j];
}
}
try
{
c[0] = c[0] / b[0];
d[0] = d[0] / b[0];
for (int i = 1; i < len - 1; i++)
{
c[i] = c[i] / (b[i] - a[i] * c[i - 1]);
d[i] = (d[i] - a[i] * d[i - 1]) / (b[i] - a[i] * c[i - 1]);
}
d[len - 1] = (d[len - 1] - a[len - 1] * d[len - 2]) / (b[len - 1] - a[len - 1] * c[len - 2]);
// back-substitution step
for (int i = (len - 1); i-- > 0; )
{
d[i] = d[i] - c[i] * d[i + 1];
}
return d;
}
catch(DivideByZeroException)
{
Console.WriteLine("Division by zero was attempted. Most likely reason is that ");
Console.WriteLine("the tridiagonal matrix condition ||(b*i)||>||(a*i)+(c*i)|| is not satisified.");
return null;
}
}
else
{
Console.WriteLine("Error: the matrix must be square. The vector must be the same size as the matrix length.");
return null;
}
}
}
#endregion
}
namespace BasicInterpolation
{
#region EXTENSIONS
public static class Extensions
{
// returns a list sorted in ascending order
public static List<T> SortedList<T>(this T[] array)
{
List<T> l = array.ToList();
l.Sort();
return l;
}
// returns a difference between consecutive elements of an array
public static double[] Diff(this double[] array)
{
int len = array.Length - 1;
double[] diffsArray = new double[len];
for (int i = 1; i <= len;i++)
{
diffsArray[i - 1] = array[i] - array[i - 1];
}
return diffsArray;
}
// scaled an array by another array of doubles
public static double[] Scale(this double[] array, double[] scalor, bool mult=true)
{
int len = array.Length;
double[] scaledArray = new double[len];
if (mult)
{
for (int i = 0; i < len; i++)
{
scaledArray[i] = array[i] * scalor[i];
}
}
else
{
for (int i = 0; i < len; i++)
{
if (scalor[i] != 0)
{
scaledArray[i] = array[i] / scalor[i];
}
else
{
// basic fix to prevent division by zero
scalor[i] = 0.00001;
scaledArray[i] = array[i] / scalor[i];
}
}
}
return scaledArray;
}
public static double[,] Diag(this double[,] matrix, double[] diagVals)
{
int rows = matrix.GetLength(0);
int cols = matrix.GetLength(1);
// the matrix has to be scare
if (rows==cols)
{
double[,] diagMatrix = new double[rows, cols];
int k = 0;
for (int i = 0; i < rows; i++)
for (int j = 0; j < cols; j++ )
{
if(i==j)
{
diagMatrix[i, j] = diagVals[k];
k++;
}
else
{
diagMatrix[i, j] = 0;
}
}
return diagMatrix;
}
else
{
Console.WriteLine("Diag should be used on square matrix only.");
return null;
}
}
}
#endregion
#region FOUNDATION
internal interface IInterpolate
{
double? Interpolate( double p);
}
internal abstract class Interpolation: IInterpolate
{
public Interpolation(double[] _x, double[] _y)
{
int xLength = _x.Length;
if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength)
{
x = _x;
y = _y;
}
}
// cubic spline relies on the abscissa values to be sorted
public Interpolation(double[] _x, double[] _y, bool checkSorted=true)
{
int xLength = _x.Length;
if (checkSorted)
{
if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength && Enumerable.SequenceEqual(_x.SortedList(),_x.ToList()))
{
x = _x;
y = _y;
}
}
else
{
if (xLength == _y.Length && xLength > 1 && _x.Distinct().Count() == xLength)
{
x = _x;
y = _y;
}
}
}
public double[] X
{
get
{
return x;
}
}
public double[] Y
{
get
{
return y;
}
}
public abstract double? Interpolate(double p);
private double[] x;
private double[] y;
}
#endregion
#region LINEAR
internal sealed class LinearInterpolation: Interpolation
{
public LinearInterpolation(double[] _x, double [] _y):base(_x,_y)
{
len = X.Length;
if (len > 1)
{
Console.WriteLine("Successfully set abscissa and ordinate.");
baseset = true;
// make a copy of X as a list for later use
lX = X.ToList();
}
else
Console.WriteLine("Ensure x and y are the same length and have at least 2 elements. All x values must be unique.");
}
public override double? Interpolate(double p)
{
if (baseset)
{
double? result = null;
double Rx;
try
{
// point p may be outside abscissa's range
// if it is, we return null
Rx = X.First(s => s >= p);
}
catch(ArgumentNullException)
{
return null;
}
// at this stage we know that Rx contains a valid value
// find the index of the value close to the point required to be interpolated for
int i = lX.IndexOf(Rx);
// provide for index not found and lower and upper tabulated bounds
if (i==-1)
return null;
if (i== len-1 && X[i]==p)
return Y[len - 1];
if (i == 0)
return Y[0];
// linearly interpolate between two adjacent points
double h = (X[i] - X[i - 1]);
double A = (X[i] - p) / h;
double B = (p - X[i - 1]) / h;
result = Y[i - 1] * A + Y[i] * B;
return result;
}
else
{
return null;
}
}
private bool baseset = false;
private int len;
private List<double> lX;
}
#endregion
#region CUBIC_SPLINE
internal sealed class CubicSplineInterpolation:Interpolation
{
public CubicSplineInterpolation(double[] _x, double[] _y): base(_x, _y, true)
{
len = X.Length;
if (len > 1)
{
Console.WriteLine("Successfully set abscissa and ordinate.");
baseset = true;
// make a copy of X as a list for later use
lX = X.ToList();
}
else
Console.WriteLine("Ensure x and y are the same length and have at least 2 elements. All x values must be unique. X-values must be in ascending order.");
}
public override double? Interpolate(double p)
{
if (baseset)
{
double? result = 0;
int N = len - 1;
double[] h = X.Diff();
double[] D = Y.Diff().Scale(h, false);
double[] s = Enumerable.Repeat(3.0, D.Length).ToArray();
double[] dD3 = D.Diff().Scale(s);
double[] a = Y;
// generate tridiagonal system
double[,] H = new double[N-1, N-1];
double[] diagVals = new double[N-1];
for (int i=1; i<N;i++)
{
diagVals[i-1] = 2 * (h[i-1] + h[i]);
}
H = H.Diag(diagVals);
// H can be null if non-square matrix is passed
if (H != null)
{
for (int i = 0; i < N - 2; i++)
{
H[i, i + 1] = h[i + 1];
H[i + 1, i] = h[i + 1];
}
double[] c = new double[N + 2];
c = Enumerable.Repeat(0.0, N + 1).ToArray();
// solve tridiagonal matrix
TridiagonalMatrix.Tridiagonal le = new TridiagonalMatrix.Tridiagonal();
double[] solution = le.Solve(H, dD3);
for (int i = 1; i < N;i++ )
{
c[i] = solution[i - 1];
}
double[] b = new double[N];
double[] d = new double[N];
for (int i = 0; i < N; i++ )
{
b[i] = D[i] - (h[i] * (c[i + 1] + 2.0 * c[i])) / 3.0;
d[i] = (c[i + 1] - c[i]) / (3.0 * h[i]);
}
double Rx;
try
{
// point p may be outside abscissa's range
// if it is, we return null
Rx = X.First(m => m >= p);
}
catch
{
return null;
}
// at this stage we know that Rx contains a valid value
// find the index of the value close to the point required to be interpolated for
int iRx = lX.IndexOf(Rx);
if (iRx == -1)
return null;
if (iRx == len - 1 && X[iRx] == p)
return Y[len - 1];
if (iRx == 0)
return Y[0];
iRx = lX.IndexOf(Rx)-1;
Rx = p - X[iRx];
result = a[iRx] + Rx * (b[iRx] + Rx * (c[iRx] + Rx * d[iRx]));
return result;
}
else
{
return null;
}
}
else
return null;
}
private bool baseset = false;
private int len;
private List<double> lX;
}
#endregion
class EntryPoint
{
static void Main(string[] args)
{
// code relies on abscissa values to be sorted
// there is a check for this condition, but no fix
// f(x) = 1/(1+x^2)*sin(x)
double[] ex = { -5, -3, -2, -1, 0, 1, 2, 3, 5};
double[] ey = { 0.036882, -0.01411, -0.18186, -0.42074, 0, 0.420735, 0.181859, 0.014112, -0.03688};
double[] p = {-5,-4.5,-4,-3.5,-3.2,-3,-2.8,-2.1,-1.5,-1,-0.8,0,0.65,1,1.3,1.9,2.6,3.1,3.5,4,4.5,5 };
LinearInterpolation LI = new LinearInterpolation(ex, ey);
CubicSplineInterpolation CS = new CubicSplineInterpolation(ex, ey);
Console.WriteLine("Linear Interpolation:");
foreach (double pp in p)
{
Console.Write(LI.Interpolate(pp).ToString()+", ");
}
Console.WriteLine("Cubic Spline Interpolation:");
foreach (double pp in p)
{
Console.WriteLine(CS.Interpolate(pp).ToString());
}
Console.ReadLine();
}
}
}
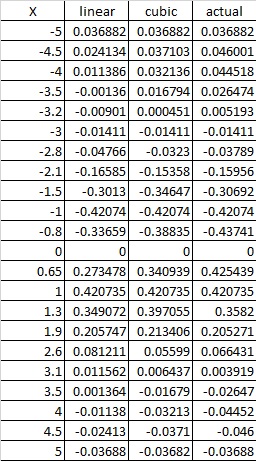
Note that I wrote a console application, and this is the reason for throwing as few exceptions as possible. Like with all the code on my blog – please feel free to take it and modify as you wish. It is now time to compare performance of linear and cubic spline interpolations on a test function: 
codefying 
Pingback: Introducing Dependency Injection into Interpolation Code | codefying